VIII - Théorie du frittage

Frittage en phase solide

La thermodynamique montre que, ce processus étant irréversible, l’enthalpie libre du système doit diminuer au cours de son évolution. Cette diminution résulte essentiellement d’une réduction de l’énergie de surface (surface libre des particules, puis surface des pores). On peut diviser le processus en deux stades: il y a d’abord formation de zones de raccordement, appelées «ponts» de soudure ou «cous» (voir paragraphe mise en forme), entre particules en contact, puis disparition progressive de la porosité résiduelle.

Formation des ponts

Les particules de poudres étant supposées sphériques, de rayon r uniforme, et tangentes entre elles, deux groupes de mécanismes ont été proposés à partir de ce modèle théorique, suivant que les centres des sphères ne se rapprochent pas (évaporation-condensation ou diffusion superficielle) ou se rapprochent (écoulement visqueux, diffusion en volume ou diffusion intergranulaire). Dans le second cas, les agglomérés présentent un retrait notable et la porosité résiduelle est progressivement éliminée.

Le mécanisme d’évaporation-condensation fut mis en évidence par W. D. Kingery lors de son étude du frittage de petites billes de chlorure de sodium. Pour établir la relation qui donne, à température donnée, la loi de croissance du rayon x du cou en fonction du temps , on tient compte du gradient de tension de vapeur qui existe entre les zones voisines de la surface convexe des sphères et les zones voisines de la surface concave du cou; on écrit alors que la variation de volume de ce cou par unité de temps est égale à la quantité de matière qui se condense à la surface de la zone de raccordement; en utilisant l’équation de Langmuir et la formule de Kelvin, on arrive à l’expression:

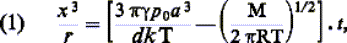
dans laquelle x est le rayon du pont, r le rayon des particules de poudres, g l’enthalpie libre superficielle spécifique du matériau constituant les granules, p₀ la pression de vapeur au voisinage d’une surface plane de ce matériau, a³ le volume d’un atome, d la densité, k la constante de Boltzmann, T la température absolue, M le poids atomique du matériau considéré, R la constante des gaz parfaits et t le temps.

On parle d’écoulement plastique si l’évolution morphologique s’opère par glissement suivant des plans et des directions cristallographiques et d’écoulement visqueux dans les autres cas. Dans l’hypothèse d’un écoulement newtonien, le déplacement des atomes s’effectue sous l’effet d’un cisaillement proportionnel au gradient de vitesse, la constante de proportionnalité étant égale à la viscosité du matériau considéré. Pour trouver la loi de croissance d’un pont, on écrit que l’énergie dissipée par l’écoulement du matériau:

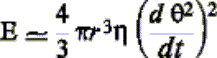
  (d’après Frenkel) est égale au travail effectué par les forces de surface, soit:

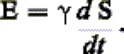
En intégrant, il vient:

Le mécanisme mettant en jeu la diffusion en volume est fondé sur l’existence de gradients de concentration en lacunes entre les zones situées au voisinage immédiat de la surface latérale du pont (de rayon de courbure r faible) et les zones voisines (qu’il s’agisse du volume des sphères ou de leur surface). Il existe en effet au voisinage d’une surface concave de rayon de courbure r une sursaturation (c’est-à-dire un excès de lacunes) égale à:

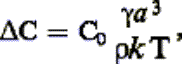
  C₀ désignant la concentration en lacunes au voisinage d’une surface plane et a³, en première approximation, le volume d’une lacune. Il suffit d’écrire que la variation de volume du pont par unité de temps est égale à celle qui résulte du départ des lacunes en excédent qui quittent la zone du pont en traversant une surface S parallèle à la surface limitant ce pont; on a:

  J étant le flux de lacunes diffusant par unité de temps et de surface. Cela suppose donc qu’il existe un gradient de lacunes entre la surface latérale du pont et une surface voisine de rayon de courbure plus grand. Comme les lacunes échangent successivement leur position avec celle des atomes voisins, on aura un flux inverse d’atomes venant constituer le pont. Il existe plusieurs hypothèses relatives à la nature du chemin suivi par les lacunes; en particulier, N. Cabrera a supposé que la diffusion s’effectuait avec une symétrie cylindrique et il a abouti à la loi:

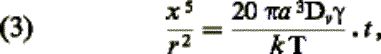
  D_v étant le coefficient d’autodiffusion en volume. Une autre hypothèse est fondée sur le fait que les lacunes diffusent en volume, en système pseudo-cylindrique, depuis la surface latérale du pont vers la surface extérieure des sphères dont le rayon de courbure est supposé rester sensiblement constant et égal à r . On aboutit à l’expression:

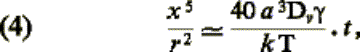
Quel que soit le trajet suivi par les lacunes, on peut noter qu’à un coefficient numérique près, x est proportionnel à t^1/5.

Ces deux hypothèses ne tiennent pas compte du rapprochement possible des centres des sphères au fur et à mesure du développement du pont. On a aussi constaté expérimentalement qu’il existait très fréquemment un joint de grain dans le pont; ce joint, séparant les volumes propres de chaque granule, a un rôle prépondérant puisqu’il sert de puits pour éliminer les lacunes; un gradient de concentration en lacunes s’établit dans le joint entre le cœur du pont et la surface externe, entraînant un flux antagoniste d’atomes qui diffusent intergranulairement vers la surface externe. Tous calculs faits, on arrive alors à:

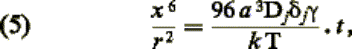
  D_j étant le coefficient d’autodiffusion aux joints et d_j l’épaisseur du joint.

Dans le mécanisme de diffusion superficielle , proposé par G. C. Kuczynski, on suppose que les lacunes excédentaires au voisinage de la surface latérale des ponts diffusent superficiellement vers la surface libre des sphères de rayon r . Des atomes de ces surfaces viennent les remplacer et contribuent de la sorte à la croissance des ponts. Les calculs proposés sont assez controversés. Kuczynski arrive à une loi de la forme:

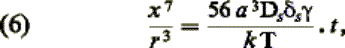
  D_s étant le coefficient d’autodiffusion superficielle et d_s l’épaisseur de la zone corticale intéressée par la diffusion.

Élimination des pores

Une fois les ponts de raccordement entre granules suffisamment développés, il existe entre eux des cavités résiduelles qu’il faut éliminer. On constate dans la pratique que, lors du frittage, la densité des agglomérés augmente progressivement en fonction du temps. Les mécanismes d’évaporation-condensation et de diffusion superficielle peuvent entraîner une modification de la morphologie des pores, mais ne peuvent pas diminuer leur volume. Seuls les mécanismes d’écoulement visqueux, de diffusion en volume et de diffusion intergranulaire peuvent rendre compte d’une telle réduction.

Les calculs sont simplifiés si l’on considère des modèles géométriques: pores cylindriques ou sphériques. Soit r le rayon d’un pore à l’instant t et r₀ son rayon initial; on arrive, par exemple, à une relation du type:

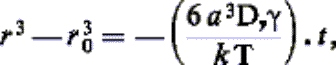
si le mécanisme entrant en jeu est l’autodiffusion en volume et les pores sphériques; les pores de petite taille disparaissent en premier et les plus gros augmentent de volume en raison de l’existence de gradients de concentration en lacunes entre les petits pores et les plus gros.

Page précédente